A team composed by researchers from NEST, Centro Mixto CSIC-UPV and Donostia International Physics Center (DIPC) (San Sebastian, Spain), Kavli Institute of Nanoscience (Delft, The Netherlands) has recently published a paper on Nature Nanotechnology journal on a phase-engineered Josephson topological materials topic.
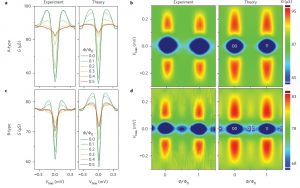
Multi-terminal superconducting Josephson junctions based on the proximity effect offer the opportunity to tailor non-trivial quantum states in nanoscale weak links. These structures can realize exotic topologies in several dimensions, for example, artificial topological superconductors that are able to support Majorana bound states and pave the way to emerging quantum technologies and future quantum information schemes. In their paper the researchers report the realization of a three-terminal Josephson interferometer based on a proximized nanosized weak link. Their tunnelling spectroscopy measurements reveal transitions between gapped (that is, insulating) and gapless (conducting) states that are controlled by the phase configuration of the three superconducting leads connected to the junction. The Authours demonstrate the topological nature of these transitions: a gapless state necessarily occurs between two gapped states of different topological indices, in much the same way that the interface between two insulators of different topologies is necessarily conducting. The topological numbers that characterize such gapped states are given by superconducting phase windings over the two loops that form the Josephson interferometer. As these gapped states cannot be transformed to one another continuously without passing through a gapless condition, they are topologically protected. The same behaviour is found for all of the points of the weak link, confirming that this topology is a non-local property.
This observation of the gapless state is pivotal for enabling phase engineering of different and more sophisticated artificial topological materials
